Kinematic Semester Review
The video above describes what you need to know from kinematics. Watch the video and make sure you understand what it is telling you. Here is a list of facts and skills that you will need to know for the semester test.
- \(\Delta x \,or\,( x – x_0)\) Displacement or final position minus initial position
- \(v_0\) Initial Velocity
- \(v\) Final Velocity
- \(a\) Acceleration
- \(t\) Time
Understand Displacement, Distance, Speed and Velocity
Displacement is the change in position and can be calculated by subtracting the final position minus the initial position or \(x-x_0\). Displacement is a vector, so a positive displacement and negative displacement indicate opposite directions.
Distance is the total path length traveled by an object. Distance is a scalar so it is always positive.
Velocity is the rate of change of position. It tells us how far an object travels in a given amount of time. Usually that means how many meters an object travels in a second. It is a vector and needs a direction. If an object is traveling in the negative direction, we need to remember to record it as a negative velocity.
An average velocity is calculated with the equation \(v_{ave}=\frac{\Delta x}{t}\) or displacement divided by time. If an object is accelerating we should not use average velocity in our kinematics equations. We will only use initial velocity and final velocity in our equations.
Speed is a scalar. It is never negative and is calculated by dividing distance by time instead of displacement.
Understand what Acceleration is and how it changes velocity based on its direction.
Acceleration is the rate of change of velocity. An object is accelerating if it is speeding up, slowing down or turning. Acceleration equals the change in velocity divided by time or \(a=\frac{\Delta v}{t}\). The acceleration is always in the same direction as the net force. If an object is speeding up, the acceleration is in the same direction as the velocity. If an object is slowing down, the acceleration is in the opposite direction as the velocity. Study the animations below to understand how the + and – signs work with acceleration and velocity.
+ Velocity + Acceleration

– Velocity + Acceleration
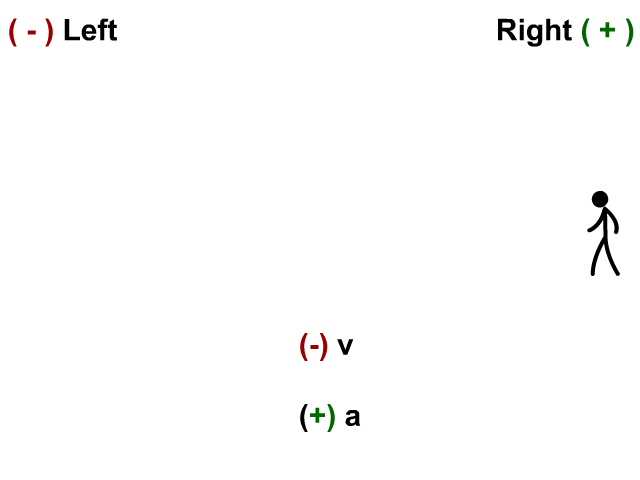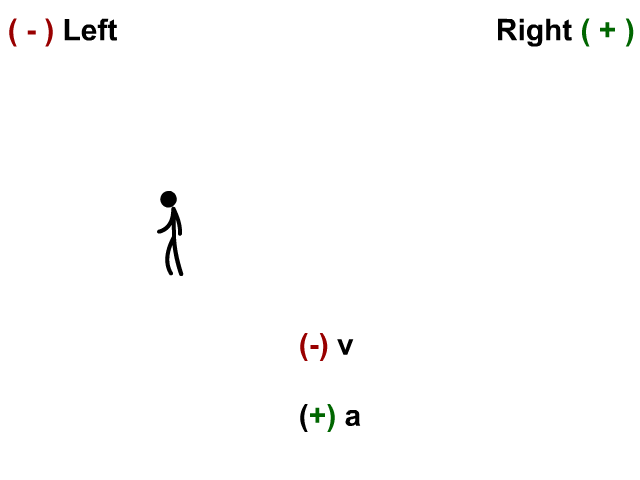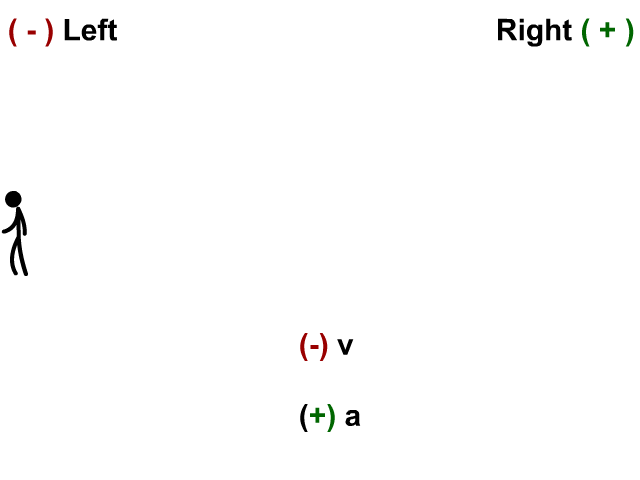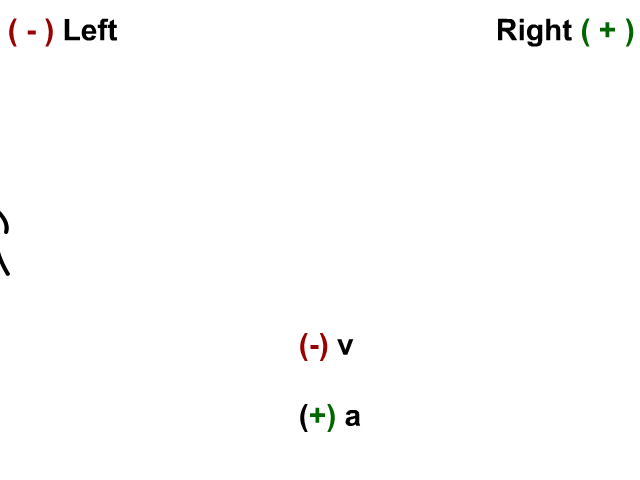
+ Velocity – Acceleration

-Velocity – Acceleration

Know the Uniformly Accelerating Motion Equations, when you should use them and the steps to solving problems with them.
You will need to memorize these equations for the semester exam.
| Linear Equations |
| \(v=v_0 + a t\) |
| \( \Delta x =v_0 t +\frac{1}{2} a t^2 \) |
| \(v^2 = v_0^2 + 2a(\Delta x)\) |
| \(\Delta x = \frac{1}{2}(v_0+v)t\) |
Kinematic Variable
The equations use five main variables, although displacement is split up on the equation sheet into initial and final position.
- \(\Delta x \,or\,( x – x_0)\) Displacement or final position minus initial position
- \(v_0\) Initial Velocity
- \(v\) Final Velocity
- \(a\) Acceleration
- \(t\) Time
When should I use these equations?
- you want to calculated one of the kinematic variables,
- you know or can figure out three of the other kinematic variables
- the acceleration is constant. (remember if the acceleration is constant then the net force is constant, for example, never use these equations with a curved ramp, because the net force and acceleration would not be constant)
Steps for solving kinematics problems
- Define a coordinate system. (positive and negative direction).
- List known and unknown variables.
- Choose an equation.
- Solve
Know these facts about Kinematic Graphs and be able to make basic calculations.
- The slope of a position time graph is the velocity.
- The slope of a velocity time graph is the acceleration.
- The area under a velocity time graph is the change in position.
- The area under the acceleration time graph is the change in velocity.
You will also need to know how to interpret kinematic graphs of motion. This interactive simulation from the physics classroom can help you practice interpreting graphs.
Projectile Motion
Remember that the vertical and horizontal motions are independent. There is acceleration in the vertical direction but not the horizontal. You will need to know how to split a projectile motion problem into components, and fill in a table of information, but you will not need to actually solve and problems. The first part of this video talks you through what you need to know, but again, you will not actually need to solve any projectile motion problem.

