Average Angular Velocity
Learning Objectives
- Be able to define and calculate average angular velocity.
- Be able to convert revolutions per minute with radians per second.
- Be able to calculate a tangential velocity from the radius and angular velocity.
| Definition | Symbol and Equation | SI Units | |
| Angular Velocity | The average angular velocity is a change in angular displacement(how far an object spins) divided by time. | \(\omega_{ave} =\displaystyle \frac {\Delta\theta}{t} \) | \(\displaystyle \frac{rad}{s}\) |
| Tangential Velocity | The velocity in meters per second that an object has moving in a circular path. Sometimes this is called linear velocity even though it is moving in a circle. | \(v =\displaystyle \omega r\) | \(\displaystyle \frac{m}{s}\) |
Angular Velocity
In linear or translational quantities, average velocity’s equation is \(V_{ave} =\displaystyle \frac {\Delta x}{t} \) or a change in position over time. It measures how fast an object is moving in meters per second. In our rotational world, average angular velocity is \(\omega_{ave} =\displaystyle \frac {\Delta\theta}{t} \) or an angular distance divided by time. It measures how fast an object is spinning. Watch the flipping physics video below to help understand the topic.
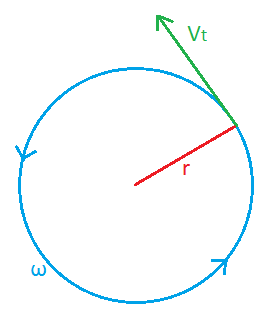
Tangential Velocity
\(v=\displaystyle \omega\, r\)
Tangential velocity is something we have already dealt with in circular motion. Sometimes we will call it linear velocity or just velocity but it means the speed of something traveling in a circle. We calculated it in the past with the equation \(v=\displaystyle \frac{2\pi r}{T}\) . If we measure our angle in radians we can make a new equation, \(\\v=\displaystyle \omega\, r\). Just like arc length, there are some instances when the tangential velocity and the velocity of the center of mass are linked. A rolling object that is not slipping is one example. In these cases the tangential velocity is the same as the velocity for the center of mass or the translational velocity.
Sample Problem
A car has tires with a radius of .3m and is traveling at a velocity of 27m/s. What is the angular velocity of the tires?
If an object is rolling with out slipping then its translational velocity is the same as the tangential velocity. Remember that translational velocity is the velocity of the center of mass. In this case because the car is moving at 27m/s we can say that the wheels have a tangential velocity of 27m/s too.
\(\\v=\displaystyle \omega\, r \\ \, \\ \omega=\displaystyle \frac{v}{r}=\displaystyle \frac{27m/s}{.3m} \\ \, \\ \omega=90\frac{rad}{s}\)
Assignment
Watch the video and answer the two questions asked; 1. What is the angular velocity of the large tractor tire? and 2. What is the radius of the smaller tractor tire? Show your work and check your answer with Mr. Smith before moving on to the quiz.
