Angular Kinematic Equations and Graphs

Learning Objectives

• Be able to apply the rotational kinematics graphs and equations to various problem involving rotation.
• Understand how rotational kinematics graphs can be used solve for angular accelerations, velocities and displacements.
• Understand how angular kinematics equations can be applied.

Variables and Equations

Angular Equations	Linear Equations
\(\omega=\omega_0 + \alpha t\)	\(v=v_0 + a t\)
\( \Delta \theta =\omega_0 t +\frac{1}{2} \alpha t^2 \)	\( \Delta x =v_0 t +\frac{1}{2} a t^2 \)
\(\omega^2 = \omega_0^2 + 2\alpha(\Delta \theta)\)	\(v^2 = v_0^2 + 2a(\Delta x)\)
\(\Delta \theta = \frac{1}{2}(\omega_0+\omega)t\)	\(\Delta x = \frac{1}{2}(v_0+v)t\)

\( S = \Delta \theta r \)	Distance equals angular displacement times radius.
\(v=\omega r\)	Tangential velocity equals angular velocity times radius.
\(a = \alpha r\)	Tangential acceleration equals angular acceleration times radius.

Rotational Kinematics Graphs

Graphical Sample Problem

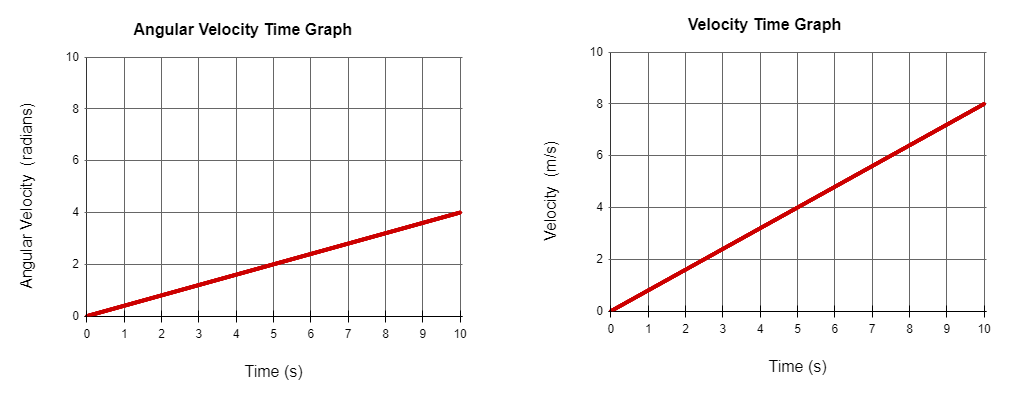
The two graphs above represent a hoop rolling down an incline without slipping. The graph on the left is the angular velocity over time. The graph on the right is the translational velocity over time. Use the slope of both graphs to calculate the radius of the hoop.

The fact that we are given linear and angular data and asked for a radius should clue us in that we should use \( a=\alpha r\). Remember that the slope of a velocity graph is the acceleration. so the angular acceleration is .4 rad/s^2 from the slope of the angular velocity graph and the linear acceleration is .8 m/s^2 from the slope of the linear velocity graph. \(\\ a=\alpha r\) so \(\\ \displaystyle r =\frac {a}{\alpha} = \frac{.8m/s^2}{.4rad/s^2}=2m\)

B.

Angular Kinematic Problem Solving

Solving angular kinematics problems is very similar to solving regular kinematic problems. Follow these steps

1. Draw a picture with relevant information
2. List all the kinematic variables you know.
3. Identify what variable you want to find.
4. Choose an equation whose only unknown variable is the variable you need to find.
5. Substitute and solve.